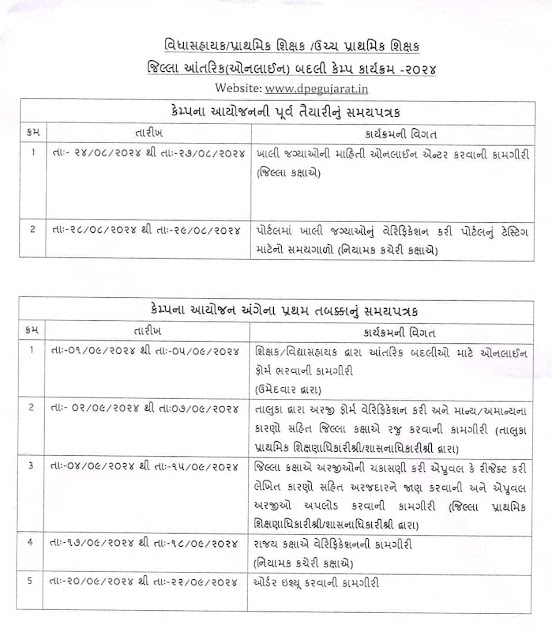
11 Maas karar CRC NI KAMGIRI SAMIXA / REVIEW PEHLA 1 MAAS NA KAMIGIRI HUKAM KARVA BABTE PARIPATRA SEE HERE

11 Maas karar CRC NI KAMGIRI SAMIXA / REVIEW PEHLA 1 MAAS NA KAMIGIRI  HUKAM KARVA BABTE PARIPATRA SEE HERE

There are several standard variations on CRCs, any or all of which may be used with any CRC polynomial. Implementation variations such as endianness and CRC presentation only affect the mapping of bit strings to the coefficients of ${\displaystyle M(x)}$ and ${\displaystyle R(x)}$, and do not impact the properties of the algorithm.

• To check the CRC, instead of calculating the CRC on the message and comparing it to the CRC, a CRC calculation may be run on the entire codeword. If the result (called the residual) is zero, the check passes. This works because the codeword is ${\displaystyle M(x)\cdot x^{n}-R(x)=Q(x)\cdot G(x)}$, which is always divisible by ${\displaystyle G(x)}$.

This simplifies many implementations by avoiding the need to treat the last few bytes of the message specially when checking CRCs.

• The shift register may be initialized with ones instead of zeroes. This is equivalent to inverting the first ${\displaystyle n}$ bits of the message feeding them into the algorithm. The CRC equation becomes ${\displaystyle M(x)\cdot x^{n}+\sum _{i=m}^{m+n-1}x^{i}=Q(x)\cdot G(x)+R(x)}$, where ${\displaystyle m>\deg(M(x))}$ is the length of the message in bits. The change this imposes on ${\displaystyle R(x)}$ is a function of the generating polynomial and the message length, ${\displaystyle \left(\sum _{i=m}^{m+n-1}x^{i}\right)\,{\bmod {\,}}G(x)}$.

The reason this method is used is because an unmodified CRC does not distinguish between two messages which differ only in the number of leading zeroes, because leading zeroes do not affect the value of ${\displaystyle M(x)}$. When this inversion is done, the CRC does distinguish between such messages.